Numeracy Skills

3. Reading & Interpreting Graphs and Charts

In this chapter, we will look at how to read and interpret the information from some of the most commonly used types of graphs and charts.

BREAK

Some important concepts and terminology

To understand this better, let's return again to the original data of the feline population of Baal, as used in the previous chapter on Mathematical Analysis:

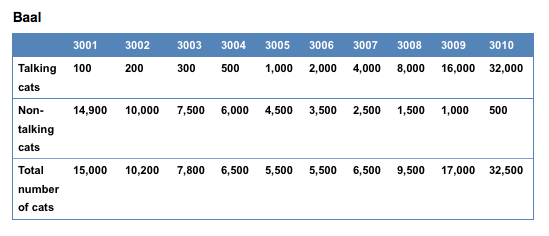
Introducing some semi-technical language here, of the kind you would be expected to use at A level, we might say that the above data - relating to talking-cats - has a range of 31,900.

Range - broadly speaking the difference between the highest and lowest number in a set - is calculated by subtracting the latter from the former (i.e. 32,000 – 100).

For the same reason, the range of data for non-talking cats is 14,400 (14,900 – 500) and the range for the total number of cats is 17,500.

BREAK

Another important concept which (ironically!) often crops up in data analysis is frequency.

‘Frequency’ relates to the rate at which a particular value occurs in any given data set. The number 5,500, for example, in the data compiled for the total number of cats, has a frequency value of 2 (it occurs twice); the value 32,500, on the other hand, only occurs once, so it has a frequency rate of 1.

BREAK

In the above table, the data which expresses the yearly increase in the talking-cat population is laid out cumulatively.

In a ‘cumulative’ setting out of data, each successive number includes (i.e. ‘adds on’) the number that precedes it.

If this data were presented so as to include only the specific yearly increases, like so:

then this would be non-cumulative. Each value is given independently of its predecessor.

BREAK

Finally, the values (variables) of any given set of data can be regarded as discrete or continuous.

A ‘discrete’ variable is one that takes on only certain values. For example, the above data is restricted to whole (cardinal) numbers. It would not be possible to include half a cat; at least not in any sense that might interest us here!

Continuous variables, in contrast, take on any value. If we were compiling data on weight, rather than amount, this would not be restricted to whole numbers alone since a cat’s mass can be continuous (2.4; 2.5; 2.6 kg etc.).

BREAK

It is worth taking some time to digest these terms before continuing.

Quick Activity

Have a go at this very short Data Quiz to make sure you've understood some of the above terminology.