Numeracy Skills

3.7. Recognising Patterns and Correlations

Patterns and correlations may well offer an indication of some causal relationship common to two sets of variables (suggesting that one data set directly created or affected another data set), but this point should never be taken for granted. (See for example cause/correlation fallacy and plausible and causal explanations)

Nevertheless, we tend to notice the apparently obvious patterns first, before properly judging their significance. Such observations can be worded along the following lines:

‘according to the figures, cases of … have fallen off steadily in line with the increasing incidence of …’ (spec.)

or,

‘according to the figures, cases of … have risen directly in line with the decreasing incidence of…’ etc.

Some examples will help us here:

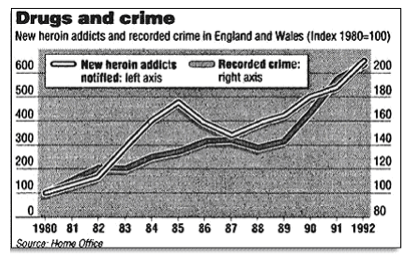
In the above line graph, a fairly clear pattern can be seen to exist between the rise in heroin addiction and recorded crime.

However, that is not to say, without further investigation, that the former causes the latter, although obviously this might offer a fairly plausible explanation. Rather, all we see at this stage is that the increase in rate of addiction coincides with that of crime.

Such an observation may well go on to support an inference (that there is a direct causal relationship; or that some third factor, for example poverty, is responsible for both rises, etc.) but at the time it is made, it is just an observation, and nothing more.

This type of correlation is said to be positive; it indicates that an increase in one variable coincides with that of another.

BREAK

Correlations can also be negative, where an increase in one variable coincides with a decrease in another:

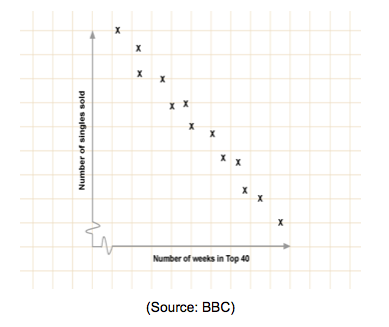
And of course there will be times when no correlation can be observed at all. Compare, for example, the following figures for the comparative international suicide rates of men and women:

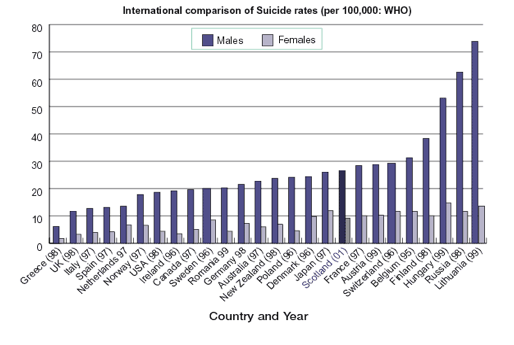
Even when the 'maths' looks like it may offer us a clear relationship, and therefore a clear explanation for the data being shown, we still need to be careful before we make any definite judgements that there are no other causes. We can only ever make plausible explanations from data correlation without definitive evidence that our conclusion is absolutely correct. Whenever you see data used in newspapers, magazines, online or in TV programs, you should listen very carefully to how that data is being used and whether the interpreter is really giving you all the facts, or just speculating or summarising the points that interest them.